Here is an amazing relation between a regular Pentagon and the golden ratio. But before going to the topic, it is necessary to understand the Ptolemy’s theorem and what the golden ratio is.
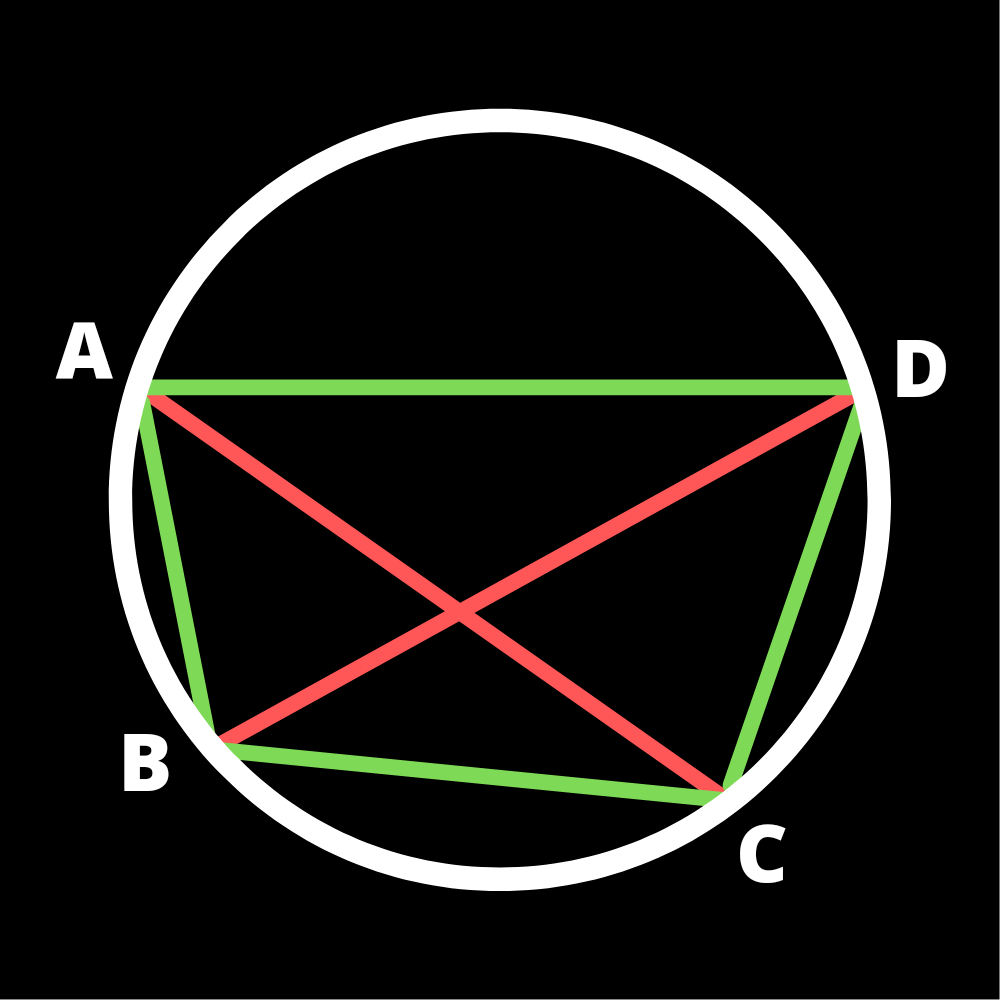
Ptolemy’s theorem
In a cyclic quadrilateral the sum of product of the opposite sides is equal to the product of the diagonals.
AB•DC + BC•AD = AC•BD
The Golden ratio
Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0
(a + b)/a = a/b = Φ
This is called the golden ratio and it’s because it has immense existence in nature and basic geometry.
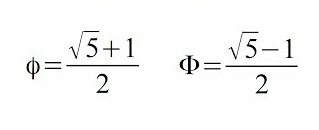
Pentagons and the golden ratio
Now coming back to today’s topic, we are interested in the ratio of the diagonal to the side of a regular pentagon. And surprisingly this ratio is equal to the golden ratio! That’s not all, we are going to prove this now.
Proof:
Apply Ptolemy’s theorem in the cyclic quadrilateral consisting of 3 sides of a regular pentagon and 1 side of diagonal of the regular pentagon.
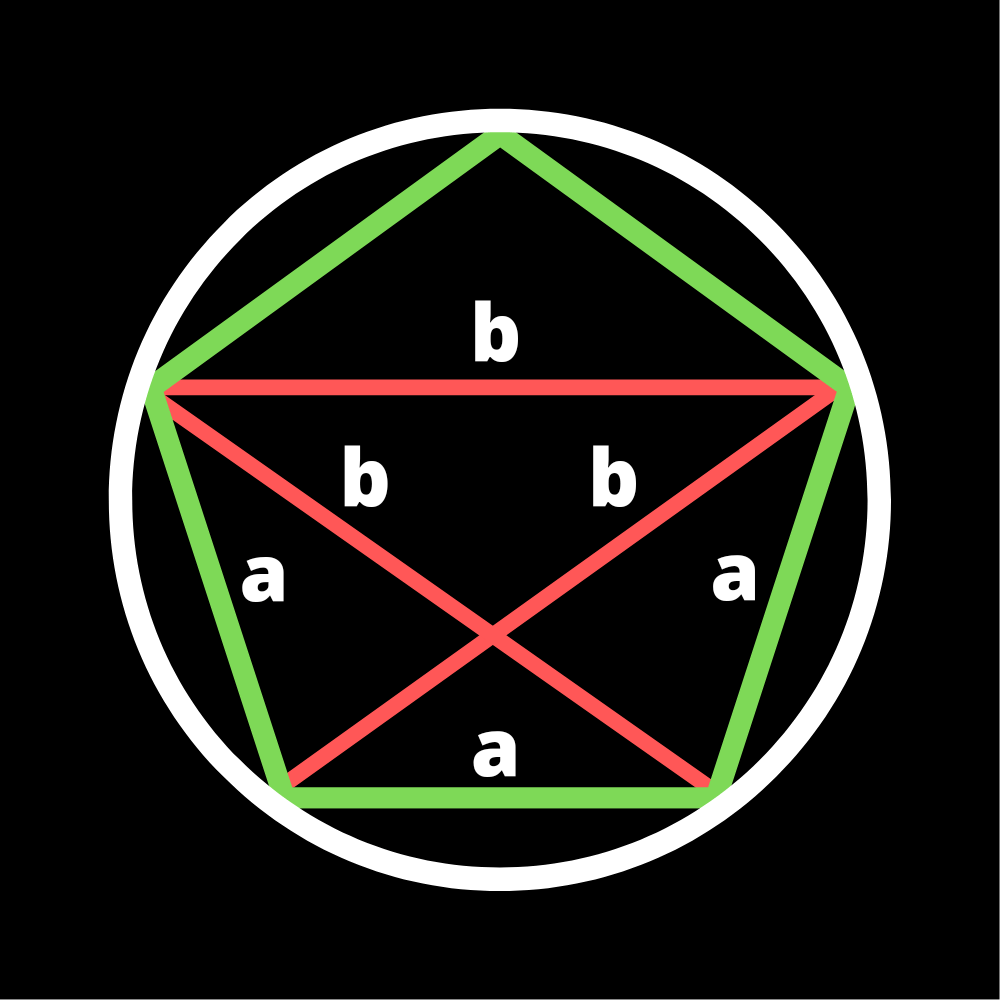
We get ab + a² = b². Divide the equation by a² and we get this quadratic equation (a/b)² – (a/b) -1 = 0. Solving this we get b/a equals the positive golden ratio!
Isn’t that amazing? Thanks for reading. For more such Wikis, puzzles and problems from mathematics share this and follow me on social platforms.
