You might have played sudoku. It’s like a mathematical grid game where you fill numbers from 1 to 9 such that no number repeats in a row as well as in a column. Buy today’s puzzle is a bit different and has additional rules.
Rules:
Take Ace, King, Queen, Jack of all colours from a deck of playing cards. The aim is to arrange them in a square 4×4 grid such that:
1. Each row, column, diagonals has an Ace, a King, a Queen, and a Jack.
2. Each row, column, diagonals has all colours of cards (a club, a hearts, a spade and a diamond).
The sample solution is shown as below:
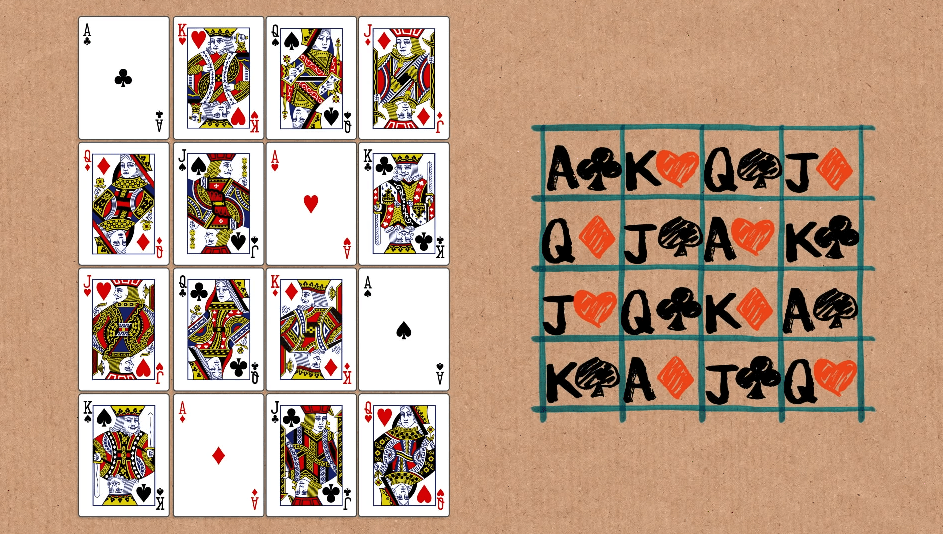
Can you solve it? And by the way in how many ways can this be solved? You can post your answers in the comment box below. (Hint: Sudoku)
Now let’s talk mathematics. This sort of arrangement is known as double Graeco-Latin Squares. We just did it for 4×4 squares but can we solve it for squares with a different dimension?
Before elaborating this let’s formalize the puzzle. Instead of playing cards with figures, let’s take cards with names A, B, C, D… (analogous to Ace, King, Queen and Jack) with numbers 1, 2, 3, 4… (analogous to colours of the cards club, spade, heart, diamond). The puzzle is for what dimension of squares can we make such Graeco-Latin Squares?
It’s possible for all squares except 2 and 6! Proving this is beyond my scope but for 2×2 grid (with card A1, A2, B1, B2) it is easy to see that if A1 occupies top left corner of the 4×4 grid no other card could be arranged according the rules laid down before because atleast one row or column or the diagonals would have repeats.
But surprisingly 6×6 grid is also impossible to solve with such conditions and was proved so by the great mathematician Euler. Hence they are called Euler Squares!
Isn’t that interesting? Thanks for reading. For more share and support Mathhexagon and follow me on social platforms!
